

If you take 30 linear steps where do you end up?
30 metres away.
If you take 30 exponential steps (2 to the power of 30) - how far will you travel?
1 billion+ metres or 26 times around the world.
What can you learn from this?
This is a story of a boy who, at age 10, read a book entitled One Thousand Ways to Make $1,000.
It started with the chapter, ‘the story of money.’
It told him how to make his first $1,000, and then how, if he grew it by 10% a year, it would ‘magically' turn into $1,600 in 5 years, $2,600 in 10, and $10,800 in 25 years.
The way these numbers exploded as they grew at a constant rate over time, was an example of how a small sum could turn into a fortune.
The boy could picture the numbers compounding as vividly as a snowball grew when he rolled it down a hill.
That boy was Warren Buffett, and the book was an introduction to the power of long-term compounding, which was about to change his life forever.
Buffet quickly announced to a friend that he would be a millionaire by age thirty-five.
He reached that target at age thirty, one billion dollars at fifty-six... and the curve shot up from there.
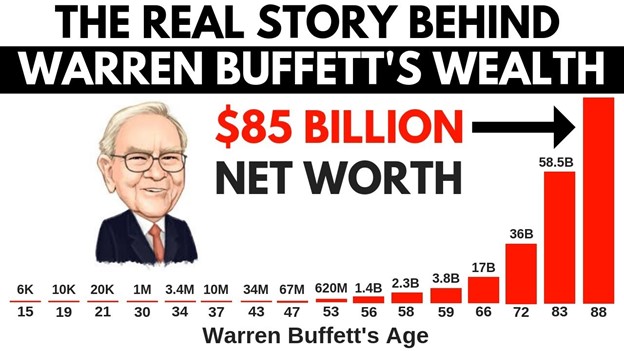
If you think Buffett’s case is a one-off act of magic, you'd be wrong.
He did nothing more than let the power of compound interest work on his money, without interrupting it at all.
In fact, the vast majority ($72billion) of his wealth has been made after the age of 65 - when most people are retired.
This power is available to each of us, but only if we understand well how it works, and then give it adequate time.
Compounding in its simplest form, means ‘interest on interest.’
So, when you invest £100 in an investment that earns 10% interest annually, you will have £110 by the end of the first year.
In the second year, the 10% interest will be calculated on £110, and so it will be £11.
This way, as the years go by, not only does the base on which your interest is calculated grow, but so does the interest itself.
So far, no magic.
But let your money grow this way over 10, 20, 30 years...
And the numbers explode, like they did in the calculation of the ten-year-old Buffett.
This is because the most powerful variable of compounding... is time.
Buffet bought his first stock at age 11, but has earned 99% of his wealth after his 50th birthday.
That's because the exponential power of compound interest gets activated only when you give it the time it requires – not months or years, but decades.
Consider this.
If you want to grow £100 to £10,000 (or 100 times) over 25 years, you need 20% annual return.
However, you'll reach only £4,000 (or 40-times of the starting £100) by the 20th year.
The remaining £6,000 (or 60-times) comes in the last five years.
That’s plain maths.
And that's why you must start rolling your snowball of savings as early as possible.
To benefit from what Buffet calls, "a really long hill".
Of course, you mustn't sacrifice your present for the sake of future.
But there is no better time to invest than yesterday...
To save as much as you can, invest that well, and then have enough patience like Ben Franklin said,
"To see your money make money, and the money that your money makes, make more money."
Compound interest is simple maths and one of the most powerful models available to us.
The best part is that it works not just on money, but on most things in life, including habits and relationships.
Start early, start small, and let time work its magic.
Meditations
"All the returns in life, whether in wealth, relationships or knowledge, come from compound interest." - Naval Ravikant
“Compound interest is the eighth wonder of the world. He who understands it, earns it … he who doesn't … pays it.” - Einstein
A question for you
In what other parts of your life could you experience compounding?
